Cadenas de Markov: o cómo medir el éxito del sueño americano.

¿Quién no ha oído hablar alguna vez del sueño americano? ¿Quién no ha soñado con querer vivirlo alguna vez? Precisamente, una de las bases que sustentan la estabilidad de la sociedad norteamericana es la igualdad de oportunidades, la idea de que cualquier individuo, aplicando esfuerzo y tesón de manera sostenida, puede llegar a prosperar y llevar una vida liberada de agobios materiales.

La movilidad social permite que, aun siendo las condiciones iniciales desfavorables, una persona pueda aspirar a un cierto nivel de bienestar acorde al devenir de los tiempos.

¿Pero qué tiene que ver todo esto con las cadenas de Markov? ¿Cómo pueden estos esquemas matemáticos ayudarnos a estudiar, por ejemplo, la sociedad americana? Hoy en el blog, haremos un experimento con modelos estadísticos para intentar entender mejor la distribución de ingresos norteamericana.

Para arrojar luz sobre esta cuestión, usaremos modelos matemáticos junto con algo de análisis de datos, con el objetivo de explorar el grado de movilidad social existente en Estados Unidos.

Vamos a generar un modelo que nos permita extraer conclusiones acerca de las probabilidades de transición entre clases sociales, partiendo únicamente de datos agregados.

Es decir, en ningún momento se observan las probabilidades de transición, sino que se infieren en base a los datos totales observados. Al final del artículo veremos algunas aplicaciones prácticas adicionales del modelo propuesto.

Las cadenas de Markov son modelos estadísticos que saltan de un estado a otro, donde la transición al siguiente estado depende exclusivamente del estado actual.

Por ejemplo, si tratamos de modelar el nivel de ingresos de una persona, podríamos incluir los eventos "nivel bajo de ingresos", "nivel medio de ingresos" y “nivel alto de ingresos” como estados, acotando cualquier comportamiento posible de un determinado individuo.

Además, en una cadena de Markov se informa acerca de la probabilidad de salto entre estados a lo largo del tiempo: por ejemplo, la probabilidad de que una persona pase del nivel bajo de ingresos al nivel más alto. El individuo iría transicionando según las probabilidades de una matriz, que podría tener esta forma:

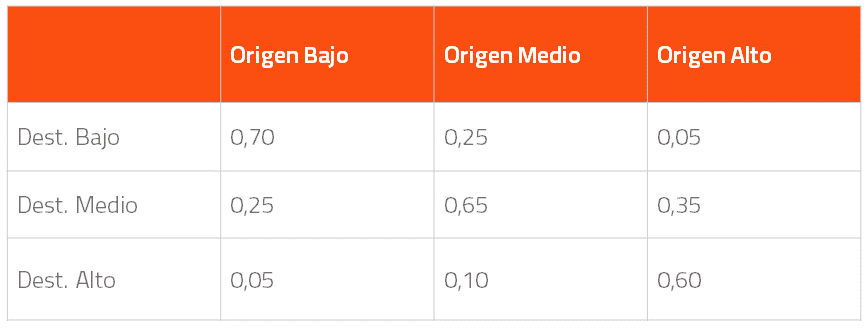
Existen distintos estados de origen y estados de destino, y en cada celda queda reflejada la probabilidad de transición entre los mismos. Por ejemplo, en la matriz anterior una persona transiciona del estado “bajo nivel de ingresos” al estado “medio nivel de ingresos” con probabilidad 0.25.

Si observáramos el número de individuos en cada grupo y lleváramos anotaciones rigurosas sobre la evolución de los mismos, podríamos intentar buscar la matriz que mejor se adapta al comportamiento observado.

Afortunadamente, la administración norteamericana lleva este recuento por nosotros, y podemos emplear datos del censo. Ahora veremos cómo se podría plantear la solución a este problema.

Análisis de movilidad social

Para comenzar, descargamos datos del censo norteamericano correspondientes al Current Population Survey durante los años de 2000 a 2016, para ambos géneros.

Obtenemos de este modo el número de hombres y mujeres en cada rango de ingresos desde 2.500 dólares al año hasta 250.000 dólares y superior. Puedes ver en este enlace un ejemplo que correspondería al año 2016.

En primer lugar, para simplificar el análisis y condicionado por el hecho de que no disponemos de muchos años para estimar el modelo, vamos a dividir los registros en tres grandes grupos: personas que ingresan menos de 100.000 dólares al año, personas entre 100.000 y 200.000 dólares, y personas que ingresan más de 200.000 dólares cada año.

Por ejemplo, para el año 2000 en el caso de los hombres tendríamos:

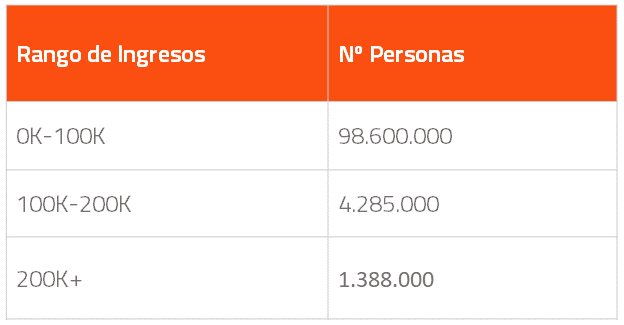
A continuación, normalizamos los datos para que representen probabilidades de pertenecer a cada rango de ingresos, por lo que el total debe sumar uno. En el ejemplo anterior daría como resultado:

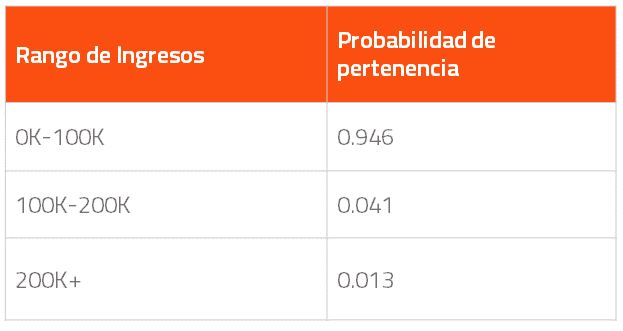
Podemos procesar de este modo todos los años involucrados y calcular la probabilidad de que un americano caiga en cada tramo en un momento dado en el tiempo, generando un fichero de entrada con este aspecto:

Se observa un incremento de ingresos a lo largo del tiempo, en este caso ocasionado tanto por mejoras en la productividad como por la inflación, que no se ha descontado de la serie y siempre se consideran las cantidades en dólares nominales.

Descontar el efecto de la inflación es un punto de mejora del presente análisis, pero complica sobremanera el mismo al tratar con tramos en lugar de registros de ingresos concretos.

Si cada grupo representa a una clase social, la pregunta que querríamos responder es: ¿cuál es la probabilidad de cambio de una clase social a otra de un año para otro? Si suponemos además, que la probabilidad de cambio depende exclusivamente de la clase social actual y es independiente de la trayectoria vital previa, lo cual es mucho suponer, podemos representar el problema mediante una cadena de Markov.

Hemos definido 3 grupos: nivel de ingresos bajo (S0), nivel de ingresos medio (S1) o alto (S2). Habiendo 3 grupos, debemos generar una matriz de transición con 9 celdas (3x3), que se presume constante a lo largo del tiempo.

La cuestión es, ¿qué matriz, de entre todas las posibles, es la que mejor explica las proporciones obtenidas a lo largo de los 17 años sujetos de estudio?

Se pueden plantear ecuaciones similares a la siguiente, que pone las proporciones del año 2001 en función de las del año 2000, relacionando las probabilidades de un año con las del año anterior, dando lugar a un total de 48 ecuaciones (3*(17-1)) para estimar un total de 9 parámetros:

Esto da lugar a un problema de optimización cuadrática, pero también se puede resolver mediante el empleo de redes neuronales. Vamos a usar Keras.

En primer lugar, tenemos que plantear las ecuaciones sujetas a optimización. Para ello desplazamos la serie temporal de la proporción a predecir un valor hacia atrás y eliminamos la columna correspondiente al año. De este modo alineamos las probabilidades de pertenencia de un año con las del año anterior.

A continuación vamos a generar una columna entera de unos, a modo de neurona de bias. Para modelar el problema, necesitaríamos crear una capa de neuronas sin entrada, donde poder aprender la matriz de transición.

Keras no lo permite, por lo que recurrimos a este pequeño subterfugio para obtener el mismo resultado.

En la capa oculta queremos aprender los pesos que corresponden a las probabilidades de transición de la cadena de Markov, por lo que la conectaremos con una capa de entrada poblada únicamente con valores constantes:

Alternativamente, si quisiéramos que las probabilidades variasen en función de ciertos atributos de entrada, la variable x_train podría ser alterada para este propósito.

Este procedimiento puede ser útil si queremos representar una cadena de Markov donde la matriz de transición no es constante a lo largo del tiempo, sino que depende de factores exógenos susceptibles de ser modelados (cadena de Markov no homogénea).

Posteriormente, definimos nuestra red neuronal capaz de aprender la matriz de transición. Utilizamos la capa oculta para modelar las 48 ecuaciones anteriores, y para garantizar que los pesos aprendidos representan probabilidades, empleamos una función de activación softmax:

De este modo generamos las salidas correspondientes a cada columna de la matriz estocástica. Finalmente, planteamos las ecuaciones y definimos como métrica de optimización el error cuadrático medio porque estamos ante un problema de regresión:

La arquitectura de la red es la siguiente. La capa inicial contiene la neurona de bias que conecta con todas las neuronas de la capa oculta, donde hay 3 funciones softmax, una por cada estado.

De este modo garantizamos que las columnas de la matriz representan probabilidades. Las probabilidades de la matriz de transición que queremos aprender vendrían representadas por las neuronas en verde.

En último término hay una última capa que efectúa un producto escalar sin función de activación y plantea las ecuaciones que vimos anteriormente, una ecuación por cada estado posible.

En cada año se efectúan 3 regresiones, donde las entradas corresponden a los estados del año anterior y las salidas corresponden a los del año en curso.

El código completo instanciaría la red llamando a la función markov_nn y ajustaría el modelo mediante el método de Keras fit.

Ejecutándolo, en función del número de épocas a entrenar, deberíamos obtener una salida como la siguiente, donde la pérdida en entrenamiento es bastante reducida:

Finalmente, a partir de la capa oculta se puede obtener la matriz de transición que mejor se ajusta a los datos de entrada:

Cada columna debe sumar 1. La primera columna hace referencia a las transiciones desde el nivel bajo de ingresos, la segunda desde el medio y la tercera, como es lógico, desde el nivel alto.

De manera análoga, las filas corresponden a los estados de destino, siendo la primera fila la correspondiente al nivel bajo de ingresos, la segunda fila la del nivel medio, y la tercera la del nivel alto.

Para los hombres, obtenemos:

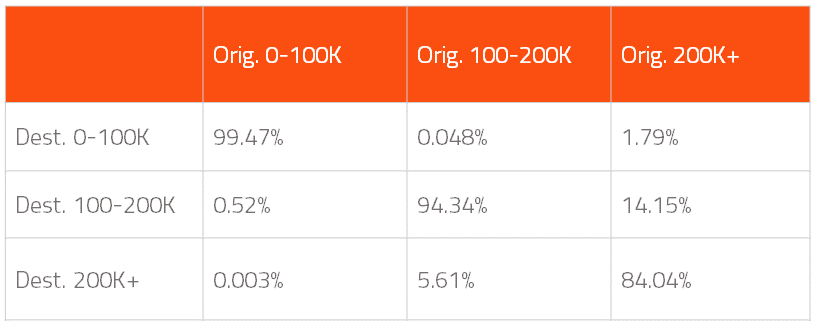
De acuerdo a la matriz, un hombre en el tramo inferior de ingresos permanece en el mismo tramo con probabilidad 0.99 de un año para otro y, en el caso de cambiar, es más probable que pase al tramo medio que al tramo alto, por lo que a primera vista los resultados parecen tener sentido.

Llama la atención la menor persistencia observada en los tramos medio y alto de ingresos, siendo la probabilidad de permanecer en el mismo tramo de 0.94 y 0.84, respectivamente.

La matriz de transición obtenida para el caso de las mujeres es la siguiente:

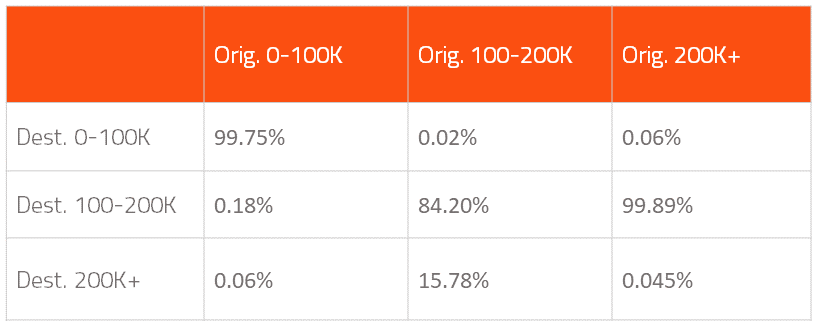
A raíz de los resultados, parece que el modelo presenta un problema porque existe escasa persistencia en el tramo alto de ingresos, cuando sería razonable pensar que de un año para otro lo normal es permanecer en el tramo de ingresos del año anterior.

Esto se puede deber a que hemos tratado de ajustar un modelo demasiado complejo para los pocos datos de los que disponemos, con lo que estaríamos ante un escenario de sobreajuste.

No obstante, podemos reducir el número de parámetros libres de 9 a 6 si modelamos la matriz de transición tratando de manera independiente la probabilidad de cambio de la probabilidad de salto a un estado concreto una vez que se produce un cambio.

Se reduce así el número de variables a estimar de orden cuadrático con el número de estados a lineal (pasando de N*N a 2*N), con lo que el esquema escala mejor en términos de grados de libertad:

La implementación de este modelo más sencillo es, paradójicamente, más compleja. Queda fuera del ámbito de este artículo, aunque también se puede programar con Keras. Si ejecutamos el nuevo modelo sobre el fichero de mujeres, obtenemos lo siguiente:

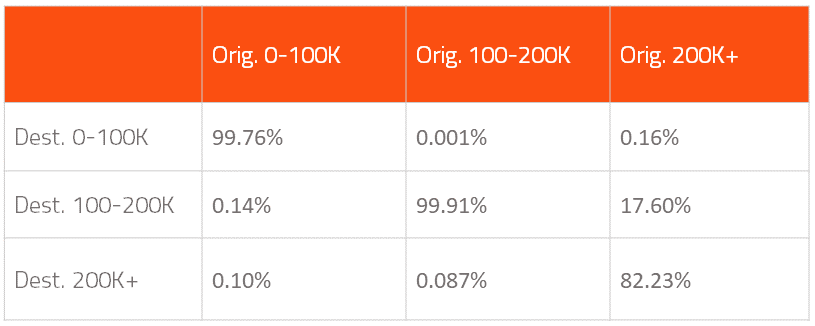
Como se puede ver hay parámetros que son muy similares a la matriz de transición con el modelo anterior, pero el global muestra mejor aspecto.

De acuerdo con nuestro modelo, la movilidad social para mujeres en Estados Unidos es sensiblemente inferior a la de los hombres y existe menor persistencia en el tramo alto de ingresos.

Estupendo, pero… ¿esto para qué vale?

Más allá del pequeño caso práctico de este artículo, podemos aplicar el presente análisis allá donde tengamos una población sujeta de estudio que pueda tomar uno entre varios estados posibles, lo cual abre el abanico de potenciales aplicaciones porque es un problema bastante de propósito general.

Lo único que necesitaríamos sería tener acceso al volumen total de individuos en cada estado a lo largo del tiempo. Veamos algunas de esas aplicaciones.

Por ejemplo, podemos tratar de predecir audiencias en televisión con cadenas de Markov, donde lo que observamos son el número de televidentes de cada cadena televisiva a lo largo del tiempo, dado que un televidente sólo puede visualizar una cadena cada vez y los estados son excluyentes.

En este caso concreto habría que interpretar el televisor apagado como uno de los estados posibles, siendo los restantes el abanico de canales de televisión disponibles en un momento dado.

También sería deseable tratar el problema como una cadena de Markov no homogénea, permitiendo variar las probabilidades según el día de la semana o la hora del día en cuestión.

Del mismo modo, dentro del sistema financiero se pueden emplear modelos similares para valorar riesgos en bonos soberanos o corporativos [1], donde intentaríamos calcular la probabilidad de que un bono de una determinada calidad crediticia subiese o bajase al siguiente escalón de las agencias de rating como Fitch o Moody’s, para tratar de estimar el riesgo incluido en una determinada cartera de inversión.

En medicina se han empleado modelos similares para analizar la evolución temporal de enfermedades crónicas como la diabetes [2], donde una persona determinada pasa de sano a enfermo crónico con una cierta probabilidad y después de un tiempo finalmente fallece.

Se pueden calibrar modelos en base al histórico y tratar de predecir la prevalencia de determinadas enfermedades proyectando la situación actual unas décadas hacia el futuro.

Y quizás más próximo al mundo de los negocios, otra posible aplicación sería tratar de estimar la lealtad a una marca, por ejemplo, en empresas de telecomunicaciones.

La pregunta que abordaríamos sería: ¿cómo de probable es que un cliente existente me abandone por un competidor determinado?

Si partimos de la premisa de que una línea de telefonía móvil sólo puede estar asociada a una compañía en cada momento, podemos interpretar las empresas como un estado posible y las opciones disponibles son claramente excluyentes.

Con lo que viendo la cuota de mercado a lo largo del tiempo, podemos plantear un escenario análogo al de los ingresos que vimos al comienzo de este artículo.

En resumen... Existe una amplia gama de aplicaciones posibles. Y tú, ¿tienes algún ejemplo en el que aplicar las cadenas de Markov?

Referencias

[1] Hull, J. C. (2003). Options futures and other derivatives. Pearson Education India. p.626-627

[2] Nazari M1, Hashemi Nazari S2, Zayeri F3, Gholampour Dehaki M4, Akbarzadeh Baghban (2018). Estimating transition probability of different states of type 2 diabetes and its associated factors using Markov model. Prim Care Diabetes. 12(3):245-253.